---

Jörg Ossenkopp, Berlin

---

 

Descartes' Mesolabium

Eine interaktive Simulation

 

In der Géométrie, [1] die René Descartes 1637 zusammen mit dem Discours de la méthode, den Météores und der Dioptrique veröffentlicht hat, taucht zweimalig eine zunächst sehr kompliziert und geheimnisvoll aussehende Zirkelkonstruktion auf, »Mesolabium« (von griechisch mésos, Mitte, und lambáno, nehmen) genannt. [2] Descartes’ Mesolabium besteht aus einem aufklappbaren und flach liegenden zweischenkligen Zirkel. Jeweils rechtwinklig zu den Schenkeln sind sechs Lineale in diesen Zirkel integriert, die einander beim Aufklappen des Zirkels verschieben (Abb. 1). [3]

Welche geometrisch-mathematische Funktion spricht Descartes diesem Mesolabium zu? Diese Frage soll im Folgenden skizzenhaft ausgeführt werden und den Kontext und Hintergrund für eine interaktive Simulation des Mesolabiums bilden (Abb. 2).

 

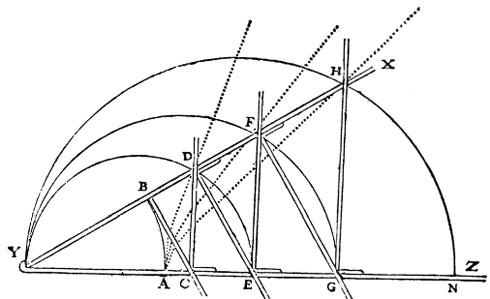
Abb. 1

 

Abb. 2

(Der obere Schenkel kann mit drag und drop bewegt werden.)

 

Zu Beginn des zweiten Kapitels seiner Geometrie stellt Descartes die Zirkelkonstruktion des Mesolabiums zuerst vor, als Abbildung mit erklärendem Text, mit deren Hilfe zusammengesetzte Kurven gezeichnet werden können und an der dann Werte für geometrische Proportionen ablesbar werden. Doch bereits 1619 nimmt Descartes in den Cogitationes privatae auf diese Zirkelkonstruktion Bezug mit den Worten »lineam circini mesolabi«. [4] Im gleichen Jahr berichtet er von ihr in einem Brief an Isaak Beeckman und zu jenem frühen Zeitpunkt seiner geometrischen Forschungen verbindet er mit ihr die Hoffnung der Lösung aller Probleme der Geometrie, die überhaupt nur lösbar sind. [5] 18 Jahre später ist Descartes dann nicht mehr so optimistisch, dennoch erscheint die Abbildung des Mesolabium-Konstrukts zweimal im Text der Geometrie.

Mit dem Mesolabium zeigt Descartes auf, wie eine systematische Einteilung von Kurven nach ihren Graden funktioniert, und er verdeutlicht, dass die nachvollziehbare Konstruierbarkeit (d.i. der antike griechische Maßstab dessen, was in die Geometrie gehört und was nicht) auch für zusammengesetzte Kurven gilt. Gleichzeitig gibt er damit ein definierendes Kriterium für die Konstruierbarkeit mathematischer Gebilde, die für ihn gerechtfertigterweise als Teil der Geometrie gelten dürfen: Es geht um die Konstruierbarkeit einer Kurve in einer homogenen, zusammenhängenden Bewegung. Schließlich ist es ihm mit Hilfe des Mesolabiums möglich, in ganz praktischer Weise geometrische Mittel-Verhältnisse zu berechnen, die das einfache Ziehen von mehrdimensionalen Wurzeln ermöglichen; und von dieser Funktion hat Descartes’ Zirkelkonstruktion ihren Namen (»Mittel-Nehmer«) erhalten.

Das Mesolabium hat somit nicht nur eine einzige Funktion, sondern derer vier:

 

1. die Berechnung von geometrischen Mitteln,

2. die Illustration der systematischen Einteilung von Kurven in Grade,

3. den Aufweis der Zugehörigkeit auch der zusammengesetzten Kurven zur Geometrie durch deren Konstruierbarkeit,

4. die Angabe eines definitorischen Kriteriums für geometrische Konstruierbarkeit in der homogenen und zusammenhängenden Bewegung der Konstruktion.

 

Berechnung von geometrischen Proportionen

Das Mesolabium hat die Eigenschaft, dass die Strecken YB, YC, YD, YE, YF, YG und YH zueinander in einer geometrischen Proportion stehen, so dass gilt:

 

YB:YC = YC:YD = YD:YE = YE:YF = YF:YG = YG:YH

 

Mehr noch, setzt man die Strecke YB als die Einheit oder, mit anderen Worten, als mit der Länge 1 versehen, und YC als x, entsprechen die entstehenden Proportionen Potenzen von x: [6]

 

1:x = x:x² = x²:x³= x³:x⁴= x⁴:x⁵= x⁵:x⁶

 

Diese Eigenschaft des Mesolabiums ist es auch, die ganz praktisch das einfache Ziehen von mehrdimensionalen Wurzeln ermöglicht. [7]

 

Illustration der systematischen Einteilung von Kurven in Grade

Die Kurven, die durch die Bewegung von D, F und H während der Öffnung des Mesolabiums entstehen und die alle ihren Ausgangspunkt in A nehmen, bezeichnet Descartes als zunehmend in ihrem Grad der Zusammengesetztheit. Denn während die Kurve AD abhängig ist von der Bewegung der Lineale BC und CD, wird die Kurve AF darüber hinaus nicht nur von der Verschiebung von BC und CD gebildet, sondern zusätzlich noch von der Verschiebung der Lineale DE und EF. Diese Form der Zusammengesetztheit dient für Descartes jedoch nur der einleitenden Illustration, denn die Einteilung, die Descartes dann tatsächlich in der Geometrie für die Klassifikation von Kurven vorschlägt, ist eine andere. [8]

 

Geometrie und die Konstruierbarkeit von zusammengesetzten Kurven

Die antiken griechischen Mathematiker teilten die geometrischen Probleme ein in ebene, körperliche und lineare. Ebene Probleme können dieser Einteilung zufolge unter Zuhilfenahme von geraden Linien und Kreisen konstruiert werden, körperliche Probleme mit Kegelschnitten, doch lineare Probleme erfordern »die Anwendung irgendeiner zusammengesetzteren Linie«. [9] Lineare Probleme wurden von den Alten als mechanisch und nicht geometrisch bezeichnet, d.h. sie wurden aus der Geometrie ausgeschlossen. Mit dem Mesolabium zeigt Descartes dagegen auf, dass nur unter Zuhilfenahme von geraden Linien und Kreisen, oder genauer: Zirkel und Lineal, zusammengesetzte Kurven erzeugt werden können, die mit einigem Gewinn in die Geometrie aufgenommen werden können. [10]

 

Kontinuierliche Bewegung als Kriterium

Descartes schlägt dementsprechend ein neues Kriterium vor für das, was in die Geometrie gehört und was nicht: die Erzeugbarkeit einer Linie durch eine Kombination von gleichartigen und kontinuierlichen Bewegungen. So wie die Kombination von Zirkel und Linealen des Mesolabiums immer zusammengesetztere Linien erzeugt, sind diese dennoch immer das Resultat einer Kombination von kontinuierlichen und gleichartigen Bewegungen. Für Descartes gehört dann nur z.B. die Quadratrix, also jene spiralförmige Kurve, die sich aus der diskontinuierlichen Kombination einer Kreisbewegung und einer geraden Bewegung ergibt, nicht mehr in den Bereich der Geometrie; die Quadratrix ist auch für Descartes mechanisch und nicht geometrisch. Zentral ist dabei, dass solche durch kontinuierliche Bewegung erzeugten Kurven immer mit einer algebraischen Gleichung beschrieben werden können. [11]

 

Konstruierbarkeit und Imagination

Descartes widerspricht also den alten griechischen Geometern, die sagen, dass Kurven, die nur mithilfe von Maschinen erzeugt werden, nicht zur Geometrie gehören, denn letztlich sind laut Descartes auch die einfachen Konstruktionshilfsmittel Lineal und Zirkel genauso Maschinen wie jede andere, kompliziertere Konstruktion auch. [12] Das Mesolabium taucht dann zwar als eine Abbildung im Text auf, die ihre eigene Konstruierbarkeit impliziert. Dennoch hat Descartes seine Zirkelkonstruktion niemals als Gegenstand gebaut und auch nicht bauen können. Ein italienisches Forschungsprojekt, das den Großteil von Descartes’ mathematischen Werkzeugen in aufwändiger handwerklicher Detailarbeit rekonstruiert hat, hat für sein Mesolabium feststellen müssen, dass bei mehr als drei Linealen, die einander verschieben sollen, der Reibungswiderstand zu groß wird, um es in den damals üblichen Materialien Holz und Metall zu realisieren. [13] Damit wird deutlich, dass das Mesolabium für Descartes ein mathematisches Konstrukt war, das vor allem in der Imagination seine Realisierung findet. [14] Die Zeichnung ist eine Konstruktionsvorlage für eine Maschine, die nur in der Imagination operiert und dementsprechend ihren mathematisch-praktischen Zweck, nämlich die Berechnung von geometrischen Mitteln, nur dort erfüllt und (mit der Notwendigkeit physikalischer Gesetze) auch nur dort erfüllen kann.

 

 

 

---

• Jean Clam: Topographie der Intersubjektivität
• Gabriele Gramelsberger: Ex Machina Symbolica
• Thomas Khurana: Maschinen der Natur
• Bernd Mahr: Pyramiden
• Johannes-Georg Schülein / Jan Wöpking: Der indirekte Augenschein

---

 

 

Downloads

Drehmomente_Ossenkopp.pdf

 

 

Endnoten