Symmetrieelemente und - operationen in Kristallen.
© PETROgraph
Einführung in die Mineral- und Gesteinsbestimmung
Kristallstruktur
Blatt 3
Die Symmetrie der Kristalle ist durch wenige Symmetrieoperationen beschreibbar:
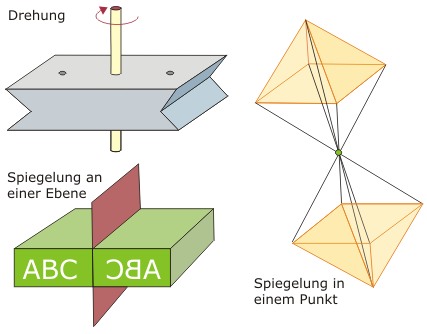
- Drehung um eine Achse
- Spiegelung durch einen Punkt
- Spiegelung an einer Ebene
Drehung: Je nachdem, wie oft das Raumgitter bei einer vollständigen Drehung um die Drehachse dieselbe geometrische Konfiguration einnimmt, werden 1-, 2-, 3- 4- und 6-zählige Achsen unterschieden. Zweizählig bedeutet, dass der Kristall um 180° gedreht werden muss, um wieder dieselbe geometrische Form zu haben. Zweizählige Achsen sind wichtige Symmetrieelemente in monoklinen und rhombischen Kristallen, dreizählige Achsen charakterisieren trigonale Kristalle, vierzählige Achsen entsprechend tetragonale und kubische Kristalle, und sechszählige Achsen hexagonale Kristalle. Einzählige Achsen kommen in triklinen Kristallen vor.
Ebenenspiegelung: Die Ebenenspiegelung erzeugt zwei identische Hälften. Sie entspricht häufig, aber nicht immer, einer Drehung um 180°.
Punktspiegelung: Die Spiegelung durch einen Punkt erzeugt zwei umgekehrt proportionale Hälften. Das Spiegelbild eines punktgespiegelten Geologenhammers würde, läge das Spiegelungszentrum am oberen Griffende, das Original am Griffenede berühren, seine Spitze würde in die andere Richtung zeigen (s. Abbildung).
Ausführliches zur Struktur und Morphologie der Kristalle erfahren Sie in der Pflichtveranstaltung Mineralogie 1.