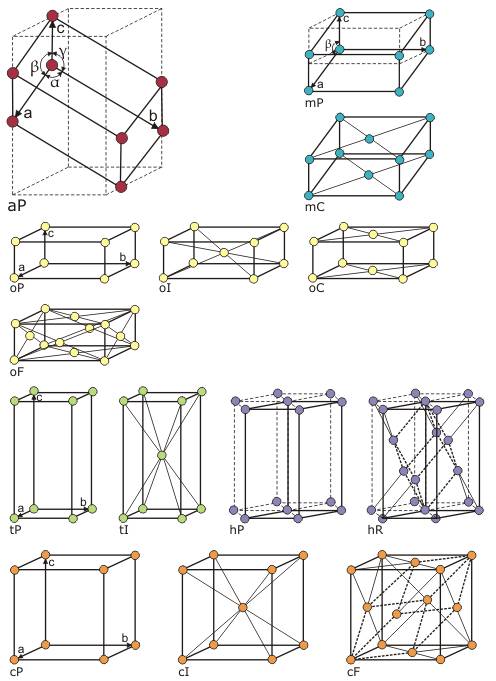
Die 14 Bravais-Gitter. Gitter aP zeigt die Grundelemente
einer Elementarzelle. © PETROgraph
einer Elementarzelle. © PETROgraph
Einführung in die Mineral- und Gesteinsbestimmung
Kristallstruktur
Blatt 2
Die Bravais-Gitter werden durch ihre Symmetrie definiert. Diese lässt sich durch die Länge ihrer drei Kanten (a, b, c) und die drei Winkel ( α, β, γ) zwischen diesen drei Kanten ausdrücken (s. Abbildung). Aus den 6 Grundtypen (die Kristallfamilien) ergeben sich durch zusätzliche Symmetrieelemente insgesamt 14 Gittertypen (s. Abbildung).
- triklin primitiv (aP): a ≠ b ≠ c, α ≠ β ≠ γ
- monoklin primitiv (mP): a ≠ b ≠ c, α = γ = 90°, β ≠ 90°
- monoklin basisflächenzentriert (mC): a b c, α = γ = 90°, β ≠ 90°
- rhombisch primitiv (oP): a ≠ b ≠ c, α = β = γ = 90°
- rhombisch innenzentriert (oI): a ≠ b ≠ c, α = β = γ = 90°
- rhombisch basisflächenzentriert (oC): a ≠ b ≠ c, α = β = γ = 90°
- rhombisch flächenzentriert (oF): a ≠ b ≠ c, α = β = γ = 90°
- tetragonal primitiv (tP): a = b ≠ c, α = β = γ = 90°
- tetragonal innenzentriert (tI): a = b ≠ c, α = β = γ = 90°
- hexagonal primitiv (hP): a = b ≠ c, α = β = 90°, γ = 120°
- hexagonal rhomboedrisch (hR): a = b ≠ c, α = β = 90°, γ = 120°
- kubisch primitiv(cP): a = b = c, α = β = γ = 90°
- kubisch innenzentriert (cI): a = b = c, α = β = γ = 90°
- kubisch flächenzentriert (cF): a = b = c, α = β = γ = 90°
Die hexagonale Kristallfamilie lässt sich morphologisch in trigonal und hexagonal unterteilen.
Weiter mit: Symmetrie von Kristallen