Mathematische Betrachtung von Wellen-die Wellengleichung Teil 2
Die mehrdimensionale Verallgemeinerung sieht so aus:
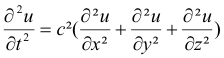
oder:
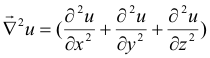
∇ symbolisiert den Nabla-Operator.
Für eine einfache harmonische Welle, die sich in der x-Richtung fortpflanzt, ergibt sich die momentane Auslenkung, a, (die maximal der Amplitude, A, entsprechen kann) durch
![]() .
.
wobei Φ die Phase der Welle ist. Erreicht zum Zeitpunkt
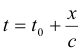
die Störung (=Auslenkung) den Ort x, gilt:
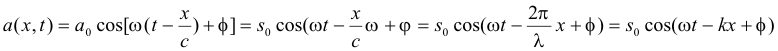
oder in komplexer Form:
![]() .
.
