Mathematische Betrachtung von Wellen-die Wellengleichung Teil 1
Die Wellengleichung ist die n-dimensionale Erweiterung der Schwingungsgleichung, die letztendlich das dritte Newtonsche Axiom (Kurzform actio est reactio; Originalzitat “Lex tertia: Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones isse mutuo semper esse aequales et in partes contrarias dirigi.” Aus: Newton, I. 1687. Philosophiae Naturalis Principia Mathematica. London) für periodische Oszillatoren ausdrückt, da bei der Ausbreitung einer Schwingung im Raum Energie und Impuls übertragen wird. Mit der Wellengleichung wird die Ausbreitung einer Welle mathematisch modelliert. Betrachten wir zunächst den eindimensionalen Fall.
Die "eindismensionale" Wellengleichung (die Zeit, t, bleibt als Dimension unberücksichtigt!) für eine Welle mit der Ausbreitungsgeschwindigkeit c ist:
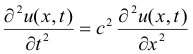
Die allgemeine Lösung, die die Auslenkung der Welle zum Zeitpunkt t beschreibt,
![]()
spaltet die Welle, entsprechend dem dritten Newtonschen Axiom, in zwei Teilwellen auf, die sich mit der gleichen Geschwindigkeit, c, nach links (-x) bzw. rechts (+x) ausbreiten. ct+x und ct-x beschreiben jeweils die Phase der Welle!
Zur Verdeutlichung füge ich hier die Beschreibung einer harmonischen Welle anhand der besprochenen wichtigen Kenngrößen (Amplitude, A, Wellenlänge, λ, Frequenz, f, Phasengeschwindigkeit, c) ein. Es gilt:
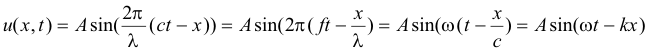
mit
- ω = Kreisfrequenz (siehe Periode)
- k = Wellenzahl; k=2πλ-1 in [m-1]
Dabei wird angenommen, dass sich die Welle in eine Richtung ausbreitet (nach x).
